Candidate generation is the first stage of recommendation. Given a query, the system generates a set of relevant candidates.
The two most common candidate generation approaches are:
Content based filtering: uses similarity between items to recommend items similar to what the user likes
Collaborative filtering: uses similarities between queries and items simultaneously to provide recommendations
Collaborative Filtering
An example of collaborative filtering would be, if user A is similar to user B, and user B likes video 1, then the system can recommend video 1 to user A (even if user A hasn't seen any videos similar to video 1)
let's take a look at an example, application of predicting movie ratings (user rates movies using 0 - stars rating system:
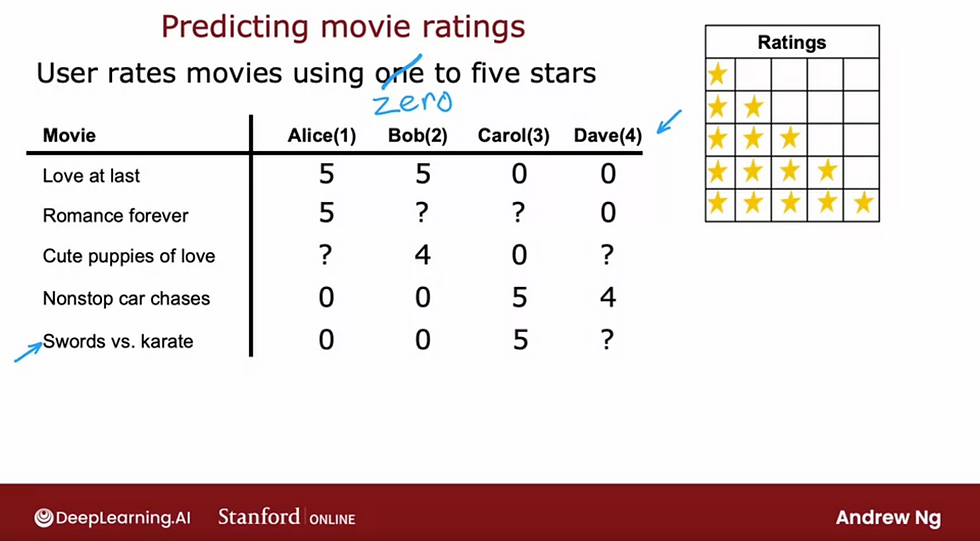
Notations we will be using (refer back to this for functions you'll see later in this article):
Nu = number of users (Nu = 4)
Nm = number of movies (Nm = 5)
r(i, j) = 1; if user j has rated movie i; e.g., r(1,1) = 1; Alice (user 1) has rated "Love at Last" (movie 1) and the assigned value is 1 for rated, 0 if has not rated.
y(i, j) = rating given by user j to the movie i; e.g., y(3, 2) = 4; Bob (user 2) rated "Cute Puppies of love" (movie 3) a rating of 4; y(i, j) can only be defined if r(i, j) == 1.
m(j) = number of movies rated by user j
n = number of features
Using per-item features
Let's take a look at how we can develop a recommender system if we had features of each item, or features of each movie using the same dataset, and add 2 additional features: x1 = romance, x2 = action
X1 denotes how much of the movie is romance and x2 denotes how much of the movie is action
We're also going to add a new notation, n = 2, as we have 2 features: x1 and x2
let's look at a few example,
x(1) being movie "Love at last" with romance of 0.9 and action of 0
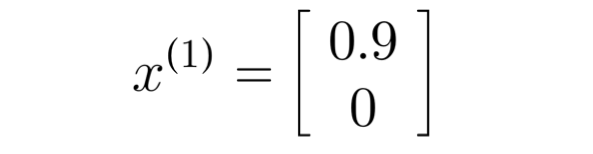
x(3) denoting movie "Cute Puppies of love" with romance of 0.99 and action of 0
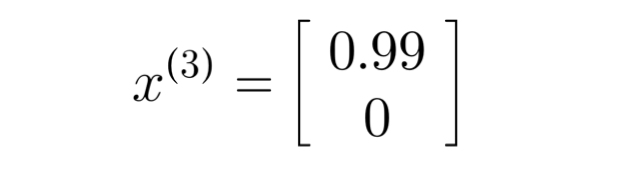
To predict user j's rating for movie i, we can use the following prediction function:
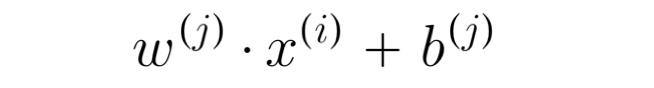
Let's user 1 (Alice) as an example to predict her potential rating for a movie she hasn't watched, movie 3 (Cute Puppies of Love):
let's say, we assign a w of 5 for romance, and 0 for action, as Alice has rated highly for other romance movies, and lower for other action movies.
for this example, we'll assign b = 0
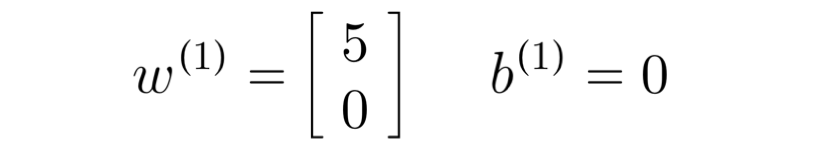
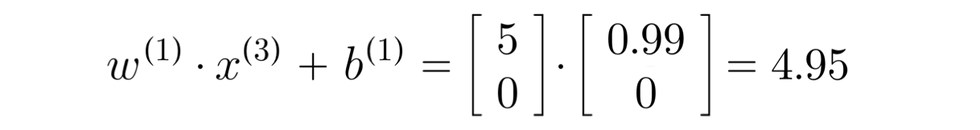
Since b is 0, we didn't add the 0 inside the calculation, the prediction predicts 4.95 out of a total rating of 5 for Alice for the movie "Cute Puppies of Love", which makes sense as she has rated 5s on other movies and 0 on action movies.
To try to calculate the dot product above, you may do so with the following code in Python:
import numpy as np
w = np.array ([5.0, 0.0])
x = np.array ([0.99, 0.0)]
res = np.dot(w, x)
print(res)Cost function to find parameters (w and b)
As we have learned in Introduction to Machine Learning , we can use a cost function to help us find the right parameters, w and b, for our users.
To compute our cost function:
We will use the prediction function, as noted above, minus the actual rating given by the user y(i, j) see notation above
We will then sum all of the movies that has been rated r(i, j) == 1 (meaning the particular user j has rated the movie)
then, if we minimize this, we should come up with a pretty good choice of parameter w(i) and b(j) for making predictions for user j's ratings
Finally, we will add our regularization term, with n = number of features, and eliminate the division by m(j) term, since it's a constant in this expression.
The cost function to learn parameters w(j), b(j) for user j:
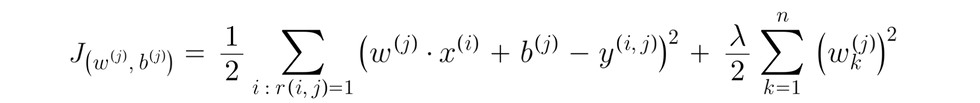
To learn parameters w(1), b(1), w(2), b(2), ..., w(Nu), b(Nu) for all users:
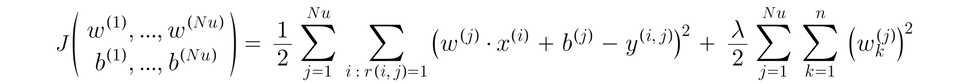
Notations:
Nu = number of users (Nu = 4 in this example)
Nm = number of movies (Nm = 5 in this example)
r(i, j) = 1; if user j has rated movie i; e.g., r(1,1) = 1; Alice (user 1) has rated "Love at Last" (movie 1) and the assigned value is 1 for rated, 0 if has not rated. (bool)
y(i, j) = rating given by user j to the movie i; e.g., y(3, 2) = 4; Bob (user 2) rated "Cute Puppies of love" (movie 3) a rating of 4; y(i, j) can only be defined if r(i, j) == 1.
m(j) = number of movies rated by user j
n = number of features
x(i) = feature vector for movie i
please note that this mathematical function starts at 1, thus j=1, etc , when you program they may start at 0 instead of 1, r(i,j) will remain equal to 1 or 0 as it's a boolean value
Collaborative Filtering Algorithm
In the above section, we have features x1(romance) and x2(action), but there will be situations where those features will not be available. In collaborative filtering, it's possible to find those features as we have ratings from multiple users of the same item with the same movie. (this is usually only possible for a system with plenty of user and movie data).
If we have parameters w and b, we can find features x through the following cost function:
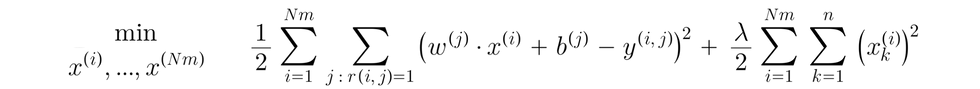
To put them together, the cost function to find w, x, and b:
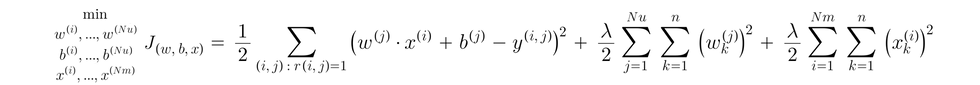
Gradient descent for collaborative filtering:
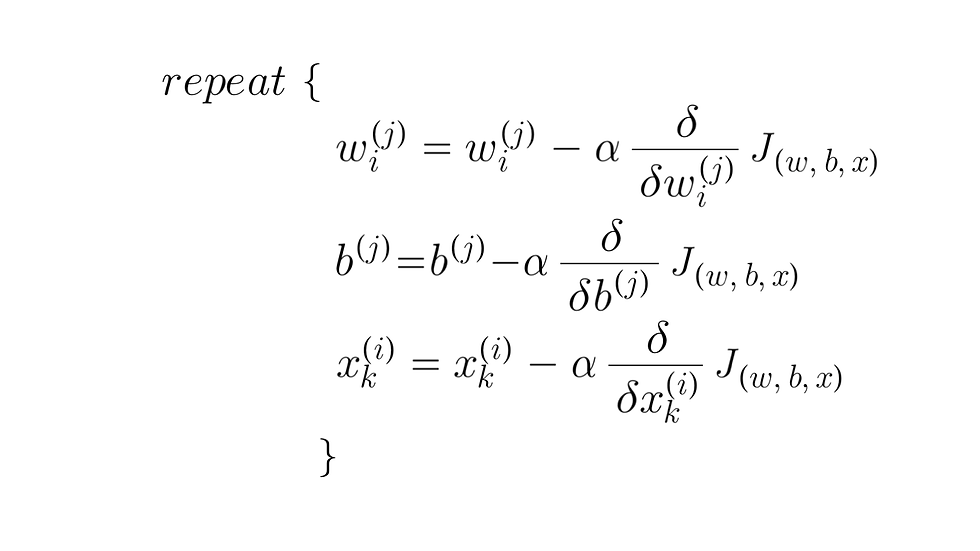
The algorithm we just did is called collaborative filtering, and the name collaborative filtering refers to the sense that because multiple users have rated the same movie collaboratively, giving you a sense if what this movie may be like, that allows you to guess the appropriate features for that movie, and this in turn, allows you to predict how other users that haven't yet rated that same movie may decide to rate it in the future.
in the next
Comments